The TPTP Format for Clausal Tableaux Proofs

by Geoff Sutcliffe, Sean Holden, Mantas Baksys

Automated Theorem Proving

Automated Theorem Proving (ATP) is concerned with the development and use of software that automates sound reasoning: the derivation of conclusions that follow inevitably from known facts. ATP is at the heart of many computational tasks, including sensitive tasks such as software/hardware verification and system security. ATP systems are often used as components of more complex Artificial Intelligence (AI) systems, which means that the impact of ATP extends into many facets of society. In many of these applications the use of ATP systems is mission critical, in the sense that incorrect results from ATP might have nasty consequences. Facing the demand for error-free results from ATP systems is the reality that ATP systems are complex pieces of software, implementing complex calculi with complex data structures and algorithms. Despite best intentions and efforts, incorrect results are possible. To counter incorrectness, an ATP system can be required to output a proof that serves as a certificate for the system's claim. To ensure that a proof is correct, proof verification can be required, which serves as a certification (but not a certificate) of the proof.

This website describes the (new) TPTP format for recording clausal tableau proofs. The format builds on the existing infrastructure of the TPTP World, in particular the TPTP format for recording derivations. An ATP system that outputs tableaux in this format is described. Existing TPTP World tools for verifying and viewing derivations can be directly extended to verify and view tableaux recorded in this new format.

Running Example

Problem

%------------------------------------------------------------------------------
fof(a1,axiom,         ! [Y] : ~ ( ~ q(Y) & ? [X] : s(X) ) ).

fof(a2,axiom,         ( r & ? [Z] : q(Z) ) => ! [X] : ~ p(X) ).

fof(a3,axiom,         p(c) | ( ~ q(c) & q(a) ) ).

fof(a4,axiom,         ~ q(c) => ! [W] : ~ q(W) ).

fof(a5,axiom,         p(c) => r ).

fof(prove,conjecture, ! [X] : ( ~ s(X) & ~ q(b) & p(c) ) ).
%------------------------------------------------------------------------------

Clause Normal Form

%------------------------------------------------------------------------------
fof(nc1,negated_conjecture,
    ~ ! [X] :
        ( ~ s(X)
        & ~ q(b)
        & p(c) ),
    inference(negate,[status(cth)],[prove]) ).

fof(nc2,negated_conjecture,
    ? [X] :
      ~ ( ~ s(X)
        & ~ q(b)
        & p(c) ),
    inference(negate,[status(thm)],[nc1]) ).

fof(nc3,negated_conjecture,
    ~ ( ~ s(sK1)
      & ~ q(b)
      & p(c) ),
    inference(skolemize,[status(esa),new_symbols(skolem,[sK1]),skolemized(X)],[nc2]) ).

cnf(c1,plain,
    ( q(Y)
    | ~ s(X) ),
    inference(clausify,[status(thm)],[a1]) ).

cnf(c2,plain,
    ( ~ q(Z)
    | ~ p(X)
    | ~ r ),
    inference(clausify,[status(thm)],[a2]) ).

cnf(c3,plain,
    ( p(c)
    | ~ q(c) ),
    inference(clausify,[status(thm)],[a3]) ).

cnf(c4,plain,
    ( p(c)
    | q(a) ),
    inference(clausify,[status(thm)],[a3]) ).

cnf(c5,plain,
    ( q(c)
    | ~ q(W) ),
    inference(clausify,[status(thm)],[a4]) ).

cnf(c6,plain,
    ( r
    | ~ p(c) ),
    inference(clausify,[status(thm)],[a5]) ).

cnf(c7,negated_conjecture,
    ( s(sK1)
    | q(b)
    | ~ p(c) ),
    inference(clausify,[status(thm)],[nc3]) ).
%------------------------------------------------------------------------------

A Closed Tableau

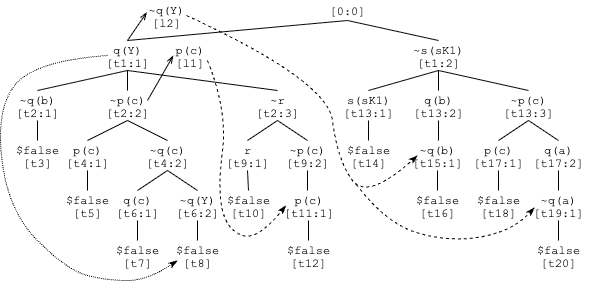
The labels in square brackets identify the literals in the annotated formulae of the TPTP the TPTP format for recording the tableau, show b elow. The dotted arrow shows the one reduction step, the solid rightward arrows point to the lemmas that are created, and the dashed arrows show where the lemmas are used. Note that lemmas can be used only below the parent node of where they are created. The tableau has the variables instantiated as they would be when the tableau is closed (but note that in general a tableau need not be ground).

TPTP Format Clausal Tableau

%------------------------------------------------------------------------------
cnf(t1,plain,
    ( q(Y)
    | ~ s(sK1) ),
    inference(start,[status(thm),parent(0:0)],[c1]) ).

cnf(t2,plain,
    ( ~ q(Y)
    | ~ p(c)
    | ~ r ),
    inference(extension,[status(thm),parent(t1:1)],[c2]) ).

cnf(t3,plain,
    $false,
    inference(connection,[status(thm),parent(t2:1)],[t2:1,t1:1]) ).

cnf(t4,plain,
    ( p(c)
    | ~ q(c) ),
    inference(extension,[status(thm),parent(t2:2)],[c3]) ).

cnf(t5,plain,
    $false,
    inference(connection,[status(thm),parent(t4:1)],[t4:1,t2:2]) ).

cnf(t6,plain,
    ( q(c)
    | ~ q(Y) ),
    inference(extension,[status(thm),parent(t4:2)],[c5]) ).

cnf(t7,plain,
    $false,
    inference(connection,[status(thm),parent(t6:1)],[t6:1,t4:2]) ).

cnf(t8,plain,
    $false,
    inference(reduction,[status(thm),parent(t6:2)],[t6:2,t1:1]) ).

cnf(l1,lemma,
    p(c),
    inference(lemma,[status(cth),parent(t2:2),below(t1:1)],[t2:2]) ).

cnf(t9,plain,
    ( r
    | ~ p(c) ),
    inference(extension,[status(thm),parent(t2:3)],[c6]) ).

cnf(t10,plain,
    $false,
    inference(connection,[status(thm),parent(t9:1)],[t9:1,t2:3]) ).

cnf(t11,plain,
    p(c),
    inference(lemma_extension,[status(thm),parent(t9:2)],[l1:1]) ).

cnf(t12,plain,
    $false,
    inference(connection,[status(thm),parent(t11:1)],[t9:2,t11:1]) ).

cnf(l2,lemma,
    ~ q(Y),
    inference(lemma,[status(cth),parent(t1:1),below(0:0)],[t1:1]) ).

cnf(t13,plain,
    ( s(sK1)
    | q(b)
    | ~ p(c) ),
    inference(extension,[status(thm),parent(t1:2)],[c7]) ).

cnf(t14,plain,
    $false,
    inference(connection,[status(thm),parent(t13:1)],[t13:1,t1:2]) ).

cnf(t15,plain,
    ~ q(b),
    inference(lemma_extension,[status(thm),parent(t13:2)],[l2:1]) ).

cnf(t16,plain,
    $false,
    inference(connection,[status(thm),parent(t15:1)],[t15:1,t13:2]) ).

cnf(t17,plain,
    ( p(c)
    | q(a) ),
    inference(extension,[status(thm),parent(t13:3)],[c4]) ).

cnf(t18,plain,
    $false,
    inference(connection,[status(thm),parent(t17:1)],[t17:1,t13:3]) ).

cnf(t19,plain,
    ~ q(a),
    inference(lemma_extension,[status(thm),parent(t17:2)],[l2:1]) ).

cnf(t20,plain,
    $false,
    inference(connection,[status(thm),parent(t19:1)],[t19:1,t17:2]) ).
%------------------------------------------------------------------------------

Representation of Clausal Tableau Proofs

There were three primary requirements for the new format for a clausal tableau:
  1. Easy reconstruction of the tableau.
  2. Sufficient information for structural verification of the closed tableau.
  3. Sufficient information for semantic verification of the inference steps.
Additional requirements are:
  1. Concise and simple enough for a natural representation of proofs.
  2. Readable by humans as well as ATP tools.

The TPTP format recognizes six inference rules, which are described below. The inference record of each annotated formula records the name of the rule used, the SZS status of the inferred formula wrt its parents, the tableau parent node, and the inference parents. The SZS status and inference parent information makes it possible to use semantic verification of each inference, and the tableau parent information makes it easy to reconstruct the tableau.

The Inference Rules

start: The initial clause below the root node. For example, in the running example t1 starts the tableau. The parent is recorded as 0:0, indicating that the node above is the root node. The logical parent of t1 is recorded as [c1]. The inference has status thm, i.e., t1 is a logical consequence of its parent. start can be viewed as a special form of extension, described next.

extension: The standard tableau extension rule. For example, in the running example t2 extends from the first literal q(b) of t1 to the 1st literal ~q(b) of c2. The parent is recorded as t1:1. The logical parent of t2 is recorded as [c2]. The inference has status thm, i.e., t2 is a logical consequence of its parent.

connection: Explicitly close the branch of the contradiction of an extension. For example, in the running example t3 closes the branch of the contradiction between q(b) and ~q(b) in the extension to t2. The parent is recorded as t2:1. The logical parents of t3 are recorded as [t2:1,t1:1], meaning the 1st literal of t2 and the 1st literal of t1. The inference has status thm, i.e., t3 is a logical consequence of its parents. connection can be viewed as a degenerate form of reduction, described next.

reduction: The standard tableau reduction rule. For example, in the running example t8 closes the branch of the contradiction between the 2nd literal ~q(b) of t6 and the 1st literal q(b) of t1. In the tableau of the running example this is denoted by the dotted arrow from q(b) to t8. The parent is recorded as t6:2. The logical parents of t8 are recorded as [t6:2,t1:1], meaning the 2nd literal of t6 and the 1st literal of t1. The inference has status thm, i.e., t8 is a logical consequence of its parents.

lemma: The creation of a unit lemma when a branch is closed. For example, in the running example l1 is the lemma p(c) created when the branch rooted at t2:2 is closed. The lemma is the negation of the 2nd literal ~p(c) of t2. Note that the role of the annotated formula records it as a lemma. The parent is recorded as t2:2. In the tableau of the running example this is denoted by the solid arrow from t2:2 to l1. As the node t1:1 is used in a reduction in closing the branch, the lemma is available only below t1:1, recorded as below(t1:1). The logical parent of l1 is recorded as [t2:2], meaning the 2nd literal ~p(c) of t2. The inference has status cth, i.e., the negation of l1 is a logical consequence of its parent.

lemma_extension: Use of a lemma to close a branch. For example, in the running example t11:1 is the lemma l1, and t12 is the connection that closes the branch down to t11:1. In the tableau of the running example this is denoted by the dashed arrow from l1 to t11:1. The lemma l1 can be used here because 9:2 is below t1:1. The parent is recorded as t11:1. The logical parent of t11 is recorded as [l1:1], meaning the 1st literal p(c) of l1. The inference has status thm, i.e., t11:1 is a logical consequence of its parent. Lemmas can be used in multiple lemma extensions. A new copy of the lemma is used each time, which provides fresh variables in the lemma. In the tableau of the running example l2 is used in the lemma extension t15, after which the variable Y is instantiated to b in the connection t16. The lemma is used again in the lemma extension t19, after which the variable Y is instantiated to a in the connection t20 lemma_extension can be viewed as a special form of extension.

Additional tableau inference rules, e.g., factorization (another view of lemma generation and use), non-unit lemma generation (also known as bottom-up lemma generation), lazy paramodulation (to deal with equality), etc., appear to be easily added to this format.

The point at which a variable becomes instantiated can optionally be recorded with a bind() record, e.g., 

cnf(t4,plain,              p(c) | ~q(c),
    inference(extension,
              [status(thm),parent(t2:2),bind(X,$fot(c))],[c3]) ).
notes that the variable X in t2 is bound to c (assuming variables have been renamed apart so that it is clear that the X is in t2).

ATP Systems and Tools

Connect++ is an ATP for first-order logic with equality, using the connection calculus to construct proofs. Connect++ implements most of the search methods and other heuristics developed for leanCoP versions 2 and later, including restricted backtracking (and an alternative version of backtracking restriction for extensions), iterative deepening by path length, various approaches to start clause selection, definitional clause conversion, deterministic or random re-ordering, and regularity testing. It also incorporates some further options such as miniscoping and polynomial-time unification. It accepts input in the TPTP cnf and fof formats. Connect++ incorporates a standard schedule similar to that of leanCoP, but also allows arbitrary schedules to be specified in a simple language. It produces certificates for proofs in a very simple format that can be verified internally, or output to a file and checked independently by a short Prolog program. From version 0.7.0 Connect++ can also produce closed tableau in the new TPTP format described in this paper. Connect++ is implemented in C++ and freely available under the GNU General Public License (GPL) Version 3. Download from www.cl.cam.ac.uk/~sbh11/connect++.html.

The extension of the GDV derivation verifier to verify tableau proofs required extending the structural verification phase, and a minor change to inference verification. Leaf verification remains unchanged, and the rule-specific steps of derivation verification are naturally inapplicable. Structural verification of a tableau proof requires checking:

Semantic verification is essentially the same as for derivations, with the small additional need to extract the specified literals from inference parents.

The IDV derivation viewer has been adapted to display tableau proofs, as the Interactive Tableau Viewer (ITV). The figure below shows the ITV rendering of the tableau in Figure~\ref{ExampleTableau}. The root node is the top $true box. Nodes from extension steps are in green-bordered ovals, $false nodes from connection and reduction steps are in red-bordered $false boxes, lemmas created in lemma steps are in blue-bordered triangles, and lemmas used in lemma_extension steps are in green-bordered triangles. ITV is available online in SystemOnTSTP, available at tptp.org/cgi-bin/SystemOnTSTP.