The ATP Process

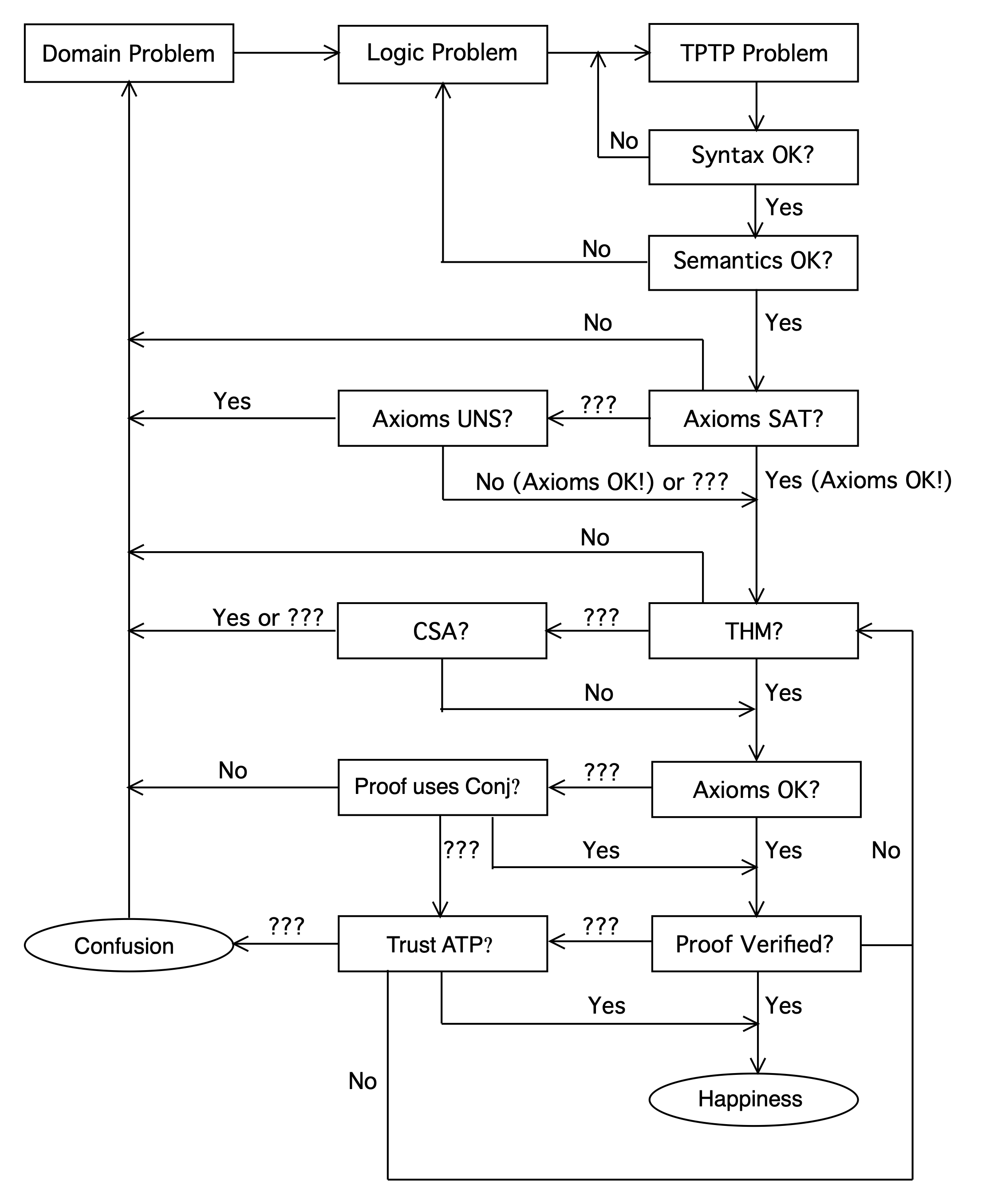
Specify the problem - the axioms and the conjecture
- Write the problem's axioms and conjecture in the domain language
- Write the problem in a logic
- Write the problem in a machine readable syntax (using a TPTP language).
- Check the syntax of the problem (using SystemB4TPTP)
  - Yes - move on to check the semantics of the problem
  - No - return to creating the machine readable file
- Check the semantics (types) of the problem (using SystemB4TPTP)
  - Yes - move on to check the consistency of the axioms
  - No - return to creating the machine readable file
Check the consistency of the axioms (using SystemOnTPTP)
- Establish that the axioms are satisfiable
  - Yes - move on to establish logical consequence
  - No - examine model/saturation, return to specify the problem
  - Unknown - establish that the axioms are unsatisfiable
- Establish that the axioms are unsatisfiable
  - Yes - examine the refutation (using IDV), return to specify the problem
  - No - move on to establish logical consequence
  - Unknown - move on to establish logical consequence (and worry)
Establish logical consequence (using SystemOnTPTP)
- Prove the theorem
  - Yes - move on to process the proof
  - No - return to specify the problem
  - Unknown - prove it's not a theorem
- Prove it's not a theorem
  - Yes - return to specify the problem
  - No - move on to processing the proof
  - Unknown - return to specify the problem
Process the proof
- Are the axioms are known to be SAT?
  - Yes - verify the proof
  - No - check if the conjecture is used in proof
  - If the axioms used in the proof are a subset of all the axioms, could check for their consistency.
- Check if the conjecture is used in proof
  - Yes - assume the axioms are OK, verify the proof
  - No - return to specify the problem
  - Unknown - ask if the ATP system is trusted
- Verify the proof (using GDV)
  - Yes - happiness
  - No - return to establish logical consequence with a different ATP system
  - Unknown - ask if the ATP system is trusted
- Is the ATP system trusted?
  - Yes - happiness
  - No - return to specify the problem
  - Unknown - confusion, return to specify the problem
Examples for the ATP Process