Example Derivation

Example Problem

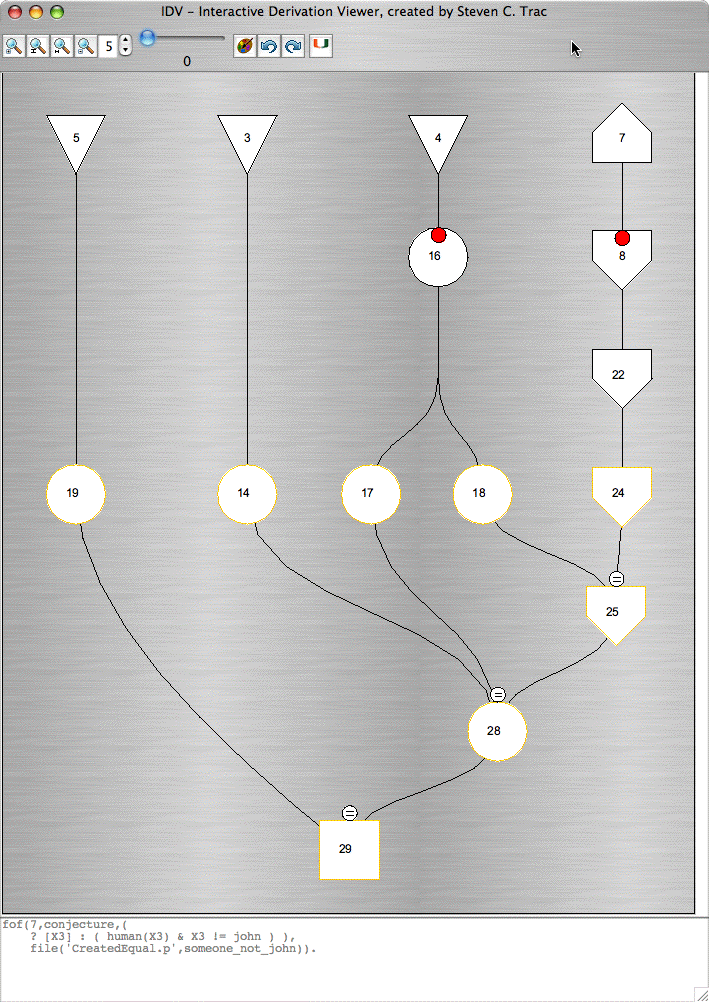
E's Proof by Refutation

fof(3,axiom,(
    grade(john) = f ),
    file('CreatedEqual.p',john_failed)).

fof(4,axiom,(
    ? [X3] : ( human(X3) & grade(X3) = a ) ),
    file('CreatedEqual.p',someone_got_an_a)).

fof(5,axiom,(
    a != f ),
    file('CreatedEqual.p',distinct_grades)).

fof(7,conjecture,(
    ? [X3] : ( human(X3) & X3 != john ) ),
    file('CreatedEqual.p',someone_not_john)).

fof(8,negated_conjecture,(
    ~ ? [X3] : ( human(X3) & X3 != john ) ),
    inference(assume_negation,[status(cth)],[7])).

cnf(14,plain,
    ( grade(john) = f ),
    inference(split_conjunct,[status(thm)],[3])).

fof(16,plain,
    ( human(esk1_0) & grade(esk1_0) = a ),
    inference(skolemize,[status(sab)],[4])).

cnf(17,plain,
    ( grade(esk1_0) = a ),
    inference(split_conjunct,[status(thm)],[16])).

cnf(18,plain,
    ( human(esk1_0) ),
    inference(split_conjunct,[status(thm)],[16])).

cnf(19,plain,
    ( a != f ),
    inference(split_conjunct,[status(thm)],[5])).

fof(22,negated_conjecture,(
    ! [X3] : ( ~ human(X3) | X3 = john ) ),
    inference(fof_nnf,[status(thm)],[8])).

cnf(24,negated_conjecture,
    ( X1 = john | ~ human(X1) ),
    inference(split_conjunct,[status(thm)],[22])).

cnf(25,negated_conjecture,
    ( john = esk1_0 ),
    inference(spm,[status(thm)],[24,18])).

cnf(28,plain,
    ( f = a ),
    inference(rw,[status(thm)],[
        inference(rw,[status(thm)],[17,25]),
        14])).

cnf(29,plain,
    ( $false ),
    inference(sr,[status(thm)],[28,19])).