A Set Theory Paradox

• The Axiom of Separation (to make set theory nice)
  • ∀Z∃Y∀X (el(X,Y) ↔ (el(X,Z) ∧ ¬el(X,X))) → ¬∃W∀U el(U,W)
  • The LHS of the → says
    • for every set Z [ ∀Z ]
    • there is a subset Y [ ∃Y∀X (el(X,Y) ↔ (el(X,Z) ]
    • containing those elements X of Z [ el(X,Z) ]
    • that are not elements of themselves [ ¬el(X,X) ]
  • The RHS of the → says
    • there does not exist a set W [ ¬∃W ]
    • such that every U is an element of W [ ∀U el(U,W) ]
    i.e., there is no universal set.

• In Classical Logic
  • The LHS is inconsistent with the existence of a universal set
  • Thus it's a theorem

• In RM3
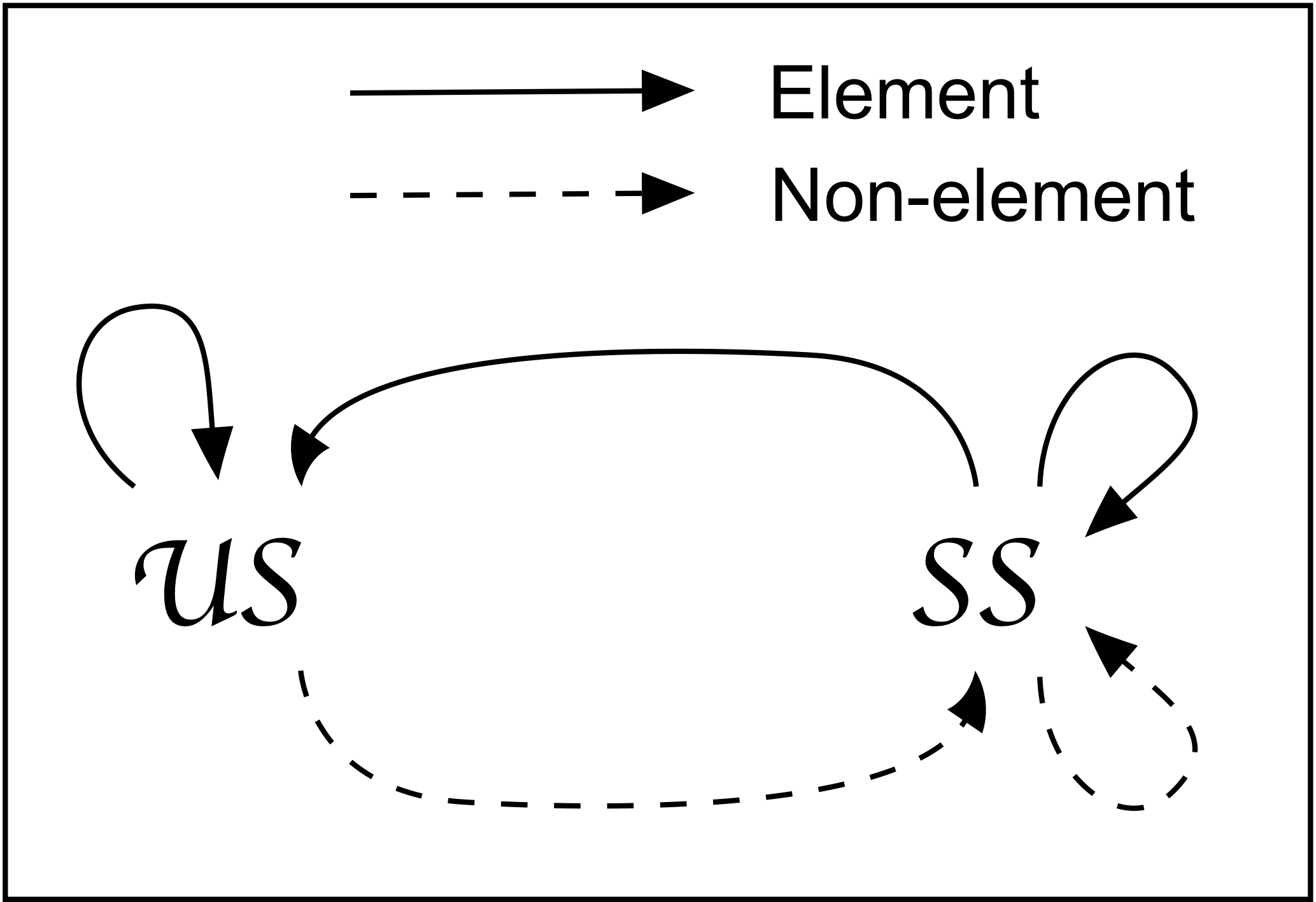
  • There is a countermodel with a domain of 2 elements {US, SS}
  • US and SS are both elements of US, so ...
       US is the Universal Set
  • US and SS are non-elements of SS, and SS is the only element of SS, so ...
       SS is the set of all sets that are not elements of themselves
  • The RHS of the → is T, and the LHS is F - it's not an RM3 theorem
  • Possible because SS can be both an element and a non-element of itself